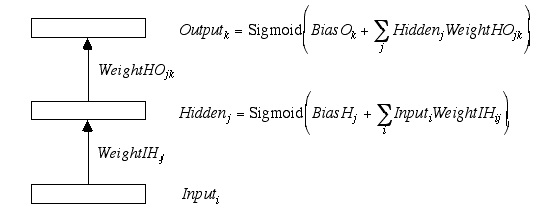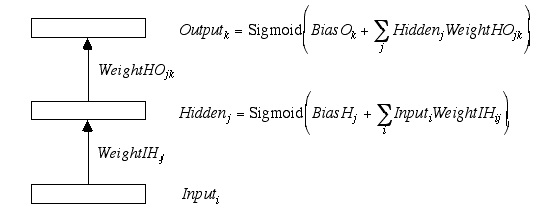John Bullinaria's Step by Step Guide to Implementing a Neural Network in C

By John A. Bullinaria from the School of Computer Science of The University of Birmingham, UK.

This document contains a step by step guide to implementing a simple neural network in C. It is aimed mainly at students who wish to (or have been told to) incorporate a neural network learning component into a larger system they are building. Obviously there are many types of neural network one could consider using - here I shall concentrate on one particularly common and useful type, namely a simple fully-connected feed-forward back-propagation network (multi layer perceptron), consisting of an input layer, one hidden layer and an output layer.

This type of network will be useful when we have a set of input vectors and a corresponding set of output vectors, and the aim is for the network to produce an appropriate output for each input it is given. Of course, if we already have a complete noise-free set of input and output vectors, then a simple look-up table would suffice. However, if we want the system to generalize, i.e. produce appropriate outputs for inputs that have never been seen before, then a neural network that has learned how to map between the known inputs and outputs (i.e. the training data set) will often do a pretty good job for new inputs as well, particularly if an appropriate regularization technique has been used.

I shall assume that the reader is already familiar with C, and for more details about neural networks in general there are plenty of good text-books and web-sites available (e.g., see my Neural Computation web-site). So, let us begin...

A single neuron (i.e. processing unit) takes its total input In and computes an associated output activation Out. A popular activation function is the sigmoid function

though other functions are often used (e.g., linear or hyperbolic tangent). This has the effect of squashing the infinite range of In into the range 0 to 1. It also has the convenient property that its derivative takes the particularly simple form

which proves useful when implementing the learning algorithm. Usually the input In into a given neuron will be the weighted sum of activations feeding in from the outputs of a number of other neurons. It is convenient to think of the activations flowing through layers of neurons. So, if there are NumInput neurons in the input layer, the total activation flowing into a hidden layer neuron is just the sum SumH over all Input[i]*Weight[i], where Weight[i] is the strength/weight of the connection between unit i in the input layer and our unit in the hidden layer. Each neuron will also have a bias, or resting state, that is added to the sum of inputs, and it is convenient to call this Weight[0]. This acts as the neuron threshold. We can then compute the hidden unit activation with

Normally the hidden layer will have many units as well, so it is appropriate to write the weights between input unit i and hidden layer unit j as an array WeightIH[i][j], in which we have added the label IH to avoid confusion with any other weights in the network. Thus to get the activation of unit j in the hidden layer we have

Remember that in C the array indices start from zero, not one, so we would declare our variables as

(or, more likely, declare pointers and use calloc or malloc to allocate the memory). Naturally, we need another loop to get all the hidden unit activations

One hidden layer is necessary and sufficient for most purposes, so our hidden layer activations will feed into the output layer in the same way as above. The code can start to become confusing at this point - keeping a separate index i, j, k for each layer helps, as does an intuitive notation for distinguishing between the different layers of weights WeightIH and WeightHO, the sums of activations feeding into each layer SumH and SumO, and the resultant activations at each layer Hidden and Output. The code thus becomes

and the network takes on the familiar form that we shall use for the remainder of this document

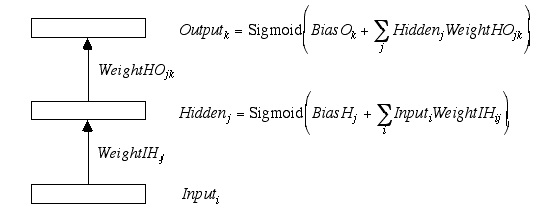
Generally we will have a whole set of NumPattern training patterns, i.e. pairs of input and target output vectors,

labelled by the index p. The network learns by minimizing some measure of the error of the network's actual outputs compared with the target outputs. For example, the sum squared error over all output units k and all training patterns p will be given by

(The factor of 0.5 is conventionally included to simplify the algebra in deriving the learning algorithm.) If we insert the above code for computing the network outputs into the p loop of this, we end up with

I'll leave the reader to dispense with any indices that they don't need for the purposes of their own system (e.g., the indices on SumH and SumO).

The next stage is to iteratively adjust the weights to minimize the network's error. A standard way to do this is by performing 'gradient descent' on the error function. We compute analytically how much the error is changed by a small change in each weight (i.e. compute the partial derivatives dError/dWeight) and shift the weights by a small amount DeltaWeight in the direction that most reduces the error. The literature is full of variations on this general approach - here we shall implemant the 'standard on-line back-propagation with momentum' algorithm. This is not the place to go through all the mathematics, but for the above sum squared error we can compute and apply one iteration (or 'epoch') of the required weight changes DeltaWeightIH and DeltaWeightHO using

(There is clearly plenty of scope for re-ordering, combining and simplifying the loops here - I will leave that for the reader to do once they have understood what the separate code sections are doing.) The weight changes DeltaWeightIH and DeltaWeightHO are each made up of two components. First, the eta component that is the gradient descent contribution, consisting of the 'learning rate' or 'step size' eta multiplied by the gradient. Second, the alpha component that is a 'momentum' term which effectively keeps a moving average of the gradient descent weight change contributions, and thus smoothes out the overall weight changes. Fixing good values of the learning parameters eta and alpha is usually a matter of trial and error. Certainly alpha must be in the range 0 to 1, and a non-zero value does usually speed up learning. However, setting alpha to zero and having no momentum allows much simpler code. Finding a good value for eta (known as the learning rate or step size) will depend on the problem, and also on the value chosen for alpha. If it is set too low, the training will be unnecessarily slow. Having it too large will cause the weight changes to oscillate wildly, and can slow down or even prevent learning altogether. (I generally start by trying eta = 0.1 and explore the effects of repeatedly doubling or halving it.)

The complete training process will consist of repeating the above weight updates for a number of epochs (using another for loop) until some error crierion is met, for example the Error falls below some chosen small number. (Note that, with sigmoids on the outputs, the Error can only reach exactly zero if the weights reach infinity! Note also that sometimes the training can get stuck in a 'local minimum' of the error function and never get anywhere the actual minimum.) So, we need to wrap the last block of code in something like

Naturally, one must set some initial network weights to start the learning process. Starting all the weights at zero is generally not a good idea, as that is often a local minimum of the error function. It is normal to initialize all the weights with small random values. If rando() is your favourite random number generator function that returns a flat distribution of random numbers in the range 0 to 1, and smallwt is the maximum absolute size of your initial weights, then an appropriate section of weight initialization code would be

Note, that it is a good idea to set all the initial DeltaWeights to zero at the same time. The best value for smallwt will depend on the problem - but they should never be so large that the sigmoids saturate before the training begins (i.e. start too close to zero or one).

If the training patterns are presented in the same systematic order during each epoch, it is possible for weight oscillations to occur. It is therefore generally a good idea to use a new random order for the training patterns for each epoch. If we put the NumPattern training pattern indices p in random order into an array ranpat[], then it is simply a matter of replacing our training pattern loop

with

Generating the random array ranpat[] is not quite so simple, but the following code will do the job

We now have enough code to put together a working neural network program. I have cut and pasted the above code into the file nn.c (which your browser should allow you to save into your own file space). I have added the standard #includes, declared all the variables, hard coded the standard XOR training data and values for eta, alpha and smallwt, #defined an overly-simple rando(), added some print statements to show what the network is doing, and wrapped the whole lot in a main(){ }. The file should compile and run in the normal way (e.g., using the UNIX commands 'cc nn.c -O -lm -o nn' and 'nn').

I've left plenty for the reader to do to convert this into a useful program, for example:

There are also numerous network variations that could usefully be implemented, for example:

But from here on, you're on your own. I hope you found this page useful...

This page is maintained by John Bullinaria. Last updated on 14 October 2009.